２変量の相関の検定( t検定)

２変量の間に相関関係があるかどうかを検定する方法で、手順は次のようになります。確率変数X,Yの間には、相関関係があるかを検定したいとします。
　
X
Y
1 x1 y1
2 x2 y2
3 x3 y3
4 x4 y4
5 x5 y5
6 x6 y6
7 x7 y7
8 x8 y8
9 x9 y9
10 x10 y10
合計 Σxi Σyi

１．まずは、仮説から…。

帰無仮説：”２変量に相関関係がない。”

対立仮説：”母平均と標本平均には差がある。”

２．有意水準 α を決め、そのときの t 分布の値 k を t 分布表より得る。

上の表からX,Yの相関係数を求めます。

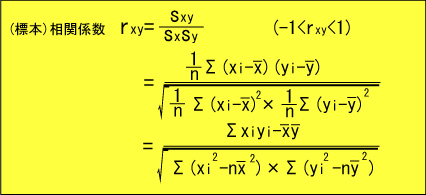
より次の検定統計量Tを計算します。

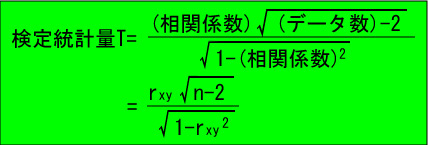
⇒　T＞k で帰無仮説を棄却し、対立仮説を採用。つまり、有意水準αで２変量には相関関係があるといえます。

例

下の表はマウスの寿命と、その子マウスの寿命を示してあります。この両者の間に相関はあるといえるか？　

　 マウスX 子マウスY X2 Y2 XY
1 940 920 883600 846400 864800
2 880 910 774400 828100 800800
3 720 850 518400 722500 612000
4 840 880 705600 774400 739200
5 1020 970 1040400 940900 989400
6 690 960 476100 921600 662400
7 920 990 846400 980100 910800
8 850 760 722500 577600 646000
9 710 900 504100 810000 639000
10
 980 940 960400 883600 921200
合計 8550 9080 7431900 8285200 7785600
仮説を立てます。

帰無仮説：”２変量に相関関係がない。”

対立仮説：”母平均と標本平均には差がある。”

有意水準α=0.05で設定し、自由度は10-2=8なので、t 分布表より2.306を得ます。

そこで、相関係数を計算します。

rxy = sxy/√(sxsy)

= (Σxy-x~y~)/√{(Σx2-nx~2)×(Σy2-ny~2)}

= (7785600-855×908)/√{(7431900-8552)(8285200-9082)}

= 7009260/√(6700875×7460736)

= 0.9913

検定統計量T = 0.9913√(10-2)/√(1-0.99132)

= 21.3

T＞k なので帰無仮説を棄却し、対立仮説を採用。つまり、有意水準α=0.05で２変量には相関関係があるといえます。

　

　２変量の相関の検定( t検定)

TOP PAGE