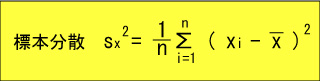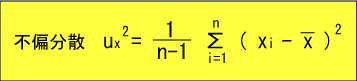統計学的指標
代表値のページでデータを一つの値であらわしてきました。しかし、この代表値だけでは、各データがそれぞれどのような散らばりを示しているのか分かりません。ばらつきを捉えるために、平均値から各データの値がどれくらい離れているかを考えればよいわけですが、単純に、
( xi - x~ )
では、正負の値が混在し、結局、
Σ( xi - x~ ) = 0
なので使い物になりません。そこで
( xi - x~ )2
を考えます。ここで、
Σ( xi - x~ )2
を偏差平方和とよびます。
偏差平方和の値は、
・ 各データの値と平均との差（ばらつき）が大きいとき
・ データ数が多いとき
に大きくなります。そこで偏差平方和をデータ数で割れば”各データと平均との差”の平均が得られます。
これらの値はデータのばらつきが大きいほど大きくなります。
標本分散は次のように変形することができ、計算する上で非常に便利です。
sx2 = 1/n・Σ( xi - x~ )2
= 1/n・Σ( xi2 - 2xix~ + x~2 )
= 1/n・Σxi2 - 2x~Σxi/n + 1/n・Σx~2
= 1/n・Σxi2 - 2x~・x~ + 1/n・nx~2
= 1/n・Σxi2 - 2x~2 + x~2
= 1/n・Σxi2 - x~2
(1/n・Σ| xi - x~ |は平均偏差と呼ばれています。）
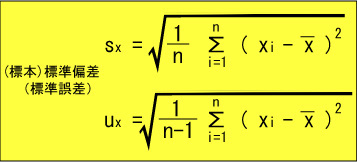
標本分散、不偏分散の単位はデータの単位と異なるため、それをあわせるために次のような指標があります。
これを利用して、各データが全体の中でどの程度かを知るために偏差値があります。
（偏差値） = 10×( xi - x~ )/ux + 50
標本平均に対応して、データのばらつきを知る指標として、標本分散が出てきました。では、中央値（メジアン）に対応するものを考えます。データ全体の中で、
小さい方から1/4の値： Q1、第１四分位、２５パーセンタイル値
小さい方から2/4の値： Q2、第2四分位、50パーセンタイル値
小さい方から3/4の値： Q3、第3四分位、7５パーセンタイル値
とそれぞれ呼び、
Q = (Q3 - Q1)/2
を四分位偏差といいます。これが、中央値に対応するばらつきの指標です。
統計学的指標
