代表値　統計学入門

データを取り扱う上でその標本の代表値を計算したりすることがよくあります。例えば、クラスの身長の平均値などもその例です。では、代表値にはどのようなものがあるのでしょうか。

代表値
（標本）平均算術平均相加平均	すべてのデータの値をたして個数nで割ったもの。	(x₁+x₂+x₃+…+x_n)/n
幾何平均相乗平均	すべてのデータの値をかけた値のn乗根。
調和平均	すべてのデータの逆数をたして個数nで割ったものの逆数。	1/{(1/x₁+1/x₂+1/x₃+…+1/x_n)/n}
中央値(メジアン）	データのちょうど真ん中の値。
最頻値（モード）	データ数が最も多い値。

ここで、３種類の平均が出てきました。算術平均、幾何平均、調和平均です。これらはどのように使い分ければよいか、例を出してみていきましょう。

・（算術）平均

平均と言えば一般にはこれですね。例を見てみましょう。

テストを行い、A君は８０点、B君は６０点、C君は７０点でした。このテストの彼らの平均点は？

これは、簡単ですね。下の図のようになります。

・幾何平均

次は幾何平均の例です。

ある会社の２年目の売り上げは初年度の３倍、３年目の売り上げは２年目の２倍でした。売り上げの伸び率の平均は？

これは、どうなるでしょう？算術平均で出すと、

( 3 + 2 )/2 = 2.5倍

となりますが、これでは駄目ですね。３年目の売り上げは初年度の３×２倍伸びています。つまり、初年度から、３年目で６倍となります。ということは、平均は

初年度から２年目：√6倍

２年目から３年目：さらに√6倍

と考えるのが自然ですね。これは下のような幾何平均で計算されます。

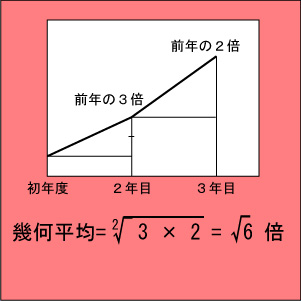
・調和平均

最後に調和平均です。

A君が3000m離れたB君の家に遊びに行くのに、行きは毎分500m、帰りは毎分300mでした。A君の平均の速さは？

これを、

( 500 + 300 )/2 = 400

としないことは、小学生でも分かります。なぜなら、A君は往復でかかった時間は、

3000/500 + 3000/300 = 16分

で、往復の距離は

3000 + 3000 = 6000m

よって、平均の速さは、

6000/16 = 375m/min

となります。これには調和平均を使います。

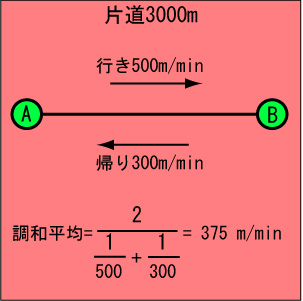
以上のように、平均にもいろいろありますが、用途によって、使い分ける必要があるのです。