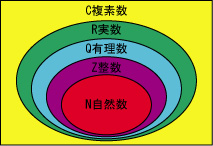
自然数に、０や負の整数を追加して、整数となり、さらに分数を追加して、有理数となります。このように数の概念が広がるにつれて、数の世界は次々に広がっていきます。

N自然数(natural numbers)

Z整数(integers)

Q有理数rational numbers

R実数(real number)

C複素数(complex numbers)

N⊂Z⊂Q⊂R⊂C

となります。図示すると、下図のようになりましたね。

ここで、無理数(irrational numbers)は実数の中でa/b(a,b∈Z)として、表記できないものでした。たとえば、√2は無理数でしたね。

ここで、中学校の教科書にも載っている、√2が無理数であることの証明をしてみましょう。

（証明）

背理法で証明する。

√2は有理数と仮定して、

√2 = a/b　(a,b∈Nかつ(a,b)=1)

とおいて、両辺を平方すると、

2 = a²/b²

⇔ a² = 2b²

両辺を比較すると、aは偶数となるので、

a=2a'

とおくと、

(2a')² = 2b²

⇔2a'² = b²

となり、この両辺も比較すると、bは偶数となる。これは、

(a,b)=1

に矛盾する。

よって、√2は無理数である。

（証明終）

これで、√2が無理数であることの確認ができました。

＜無理数の分類＞

つまり、√2や√3は代数的数です。では、代数的数ではない無理数とはどのようなものでしょうか？

超越数にはπやeが含まれます。これらが、無理数であることの証明は非常に複雑で難解なのでここでは省略します。

１８４４年フランスのリウヴィル(Joseph Liouville：1809-1882)は、初めて超越数の存在を証明しました。

その例として、

をあげ、超越数は無限にあることも示しました。

さらに、１８７３年，エルミート(Charles Hermite：1822-1901)は e が超越数であることを示し，１８８２年、リンデマン(Carl Louis Ferdinand von Lindemann：1852-1939)はπが超越数であることを示しました。

驚くべきことに、１８７７年にカントール(Georg Ferdinand Ludwig Philipp Cantor：1845-1918)は集合論を用い、超越数は代数的数よりはるかに多いことを示しました。

　

参照　循環小数(Repeating Decimal)