循環小数 Repeating Decimal

次のような循環小数を考えます。

a = 0.12323232323…

これは次のようにあらわされます。

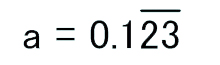
ここで上線部分を循環節といいます。

”循環小数は分数であらわすことができる”ということは中学校のときに習いましたね。aを分数であらわしてみましょう。

100a - a = 12.3232323… - 0.1232323…

99a = 12.2

a = 122/10 × 1/99

= 61/495

定理

a,b∈Nとする。このとき、
a/b

の小数展開は循環するか有限である。

（証明）

aをbで割った商をp₁、余りをq₁とすると、

a = bp₁ + q₁　( 0≦q₁≦b-1)

さらに、qをbで割った商をp₁、余りをq₁とする。以下同様にp_iおよびq_i( i = 1,2,3,…)を定めていく。

10q₁ = bp₂ + q₂　( 0≦q₂≦b-1)

10q₂ = bp₃ + q₃　( 0≦q₃≦b-1)

10q₃ = bp₄ + q₄　( 0≦q₄≦b-1)

10q₄ = bp₅ + q₅　( 0≦q₅≦b-1)

　　　…

このとき、q_j = q_k(j≠k)となった時点で、a/bは循環することが分かります。

ここで、q_iとなりうる数は0からb-1までのたかだかb個しかないわけですから、上の操作をb+1回、繰り返すと、必ずq_j = q_k(j≠k)となるj,kが存在する。

（証明終）

では、先ほどの例、61/495で試してみましょう。

61 = 495×0 + 61

610 = 495×1 + 115

1150 = 495×2 + 160

1600 = 495×3 + 115

やはり、115という数が重なってきましたね。

定理

a,b∈N,(a,b)=(10,b)=1とする。このとき、
a/b

の小数展開における循環節はord_b(10)となる。

ord（位数）に関してはこちらを参照。