連分数(Continued Fraction)

a,b∈Nとします。

aをbで割った商をp₁、余りをq₁とすると、

a = bp₁ + q₁　　　…(1)

さらに、qをbで割った商をp₁、余りをq₁とする。以下同様にp_iおよびq_i( i = 1,2,3,…)を定めていく。

b = q₁p₂ + q₂　　　…(2)

q₁ = q₂p₃ + q₃

q₂ = q₃p₄ + q₄　

q₃ = q₄p₅ + q₅

　　　…

次に(1)の両辺をbで割ると、

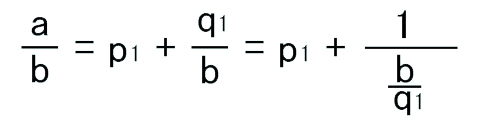　　…(3)

同様に(2)の両辺もq₁で割ると、

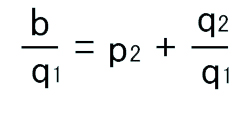
これを(3)に代入すると、

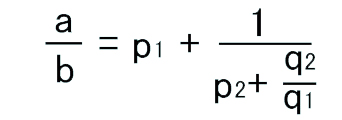
同様にして、次々と代入していくと、

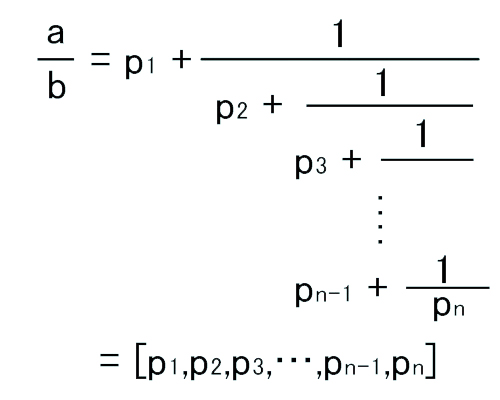
となります。

ここで、無限連分数は

[p₁,p₂,p₃,…,p_n,…]

とあらわしたりします。

次に連分数展開の例をあげます。√2を連分数展開してみましょう。

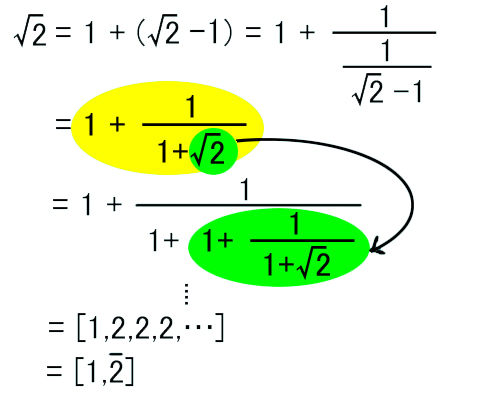この例では√2を黄色で囲ったように変形して、その黄色で囲った中の√2（緑で囲った）をそのまま黄色で置き換えて、以下同様にしていったものです。結局、√2の無限連分数展開は、[1,2,2,2,…]という循環連分数になります。

このような循環連分数を目にすると、[1,1,1,1,…]はどのような数なのか知りたくなりますよね？これは、

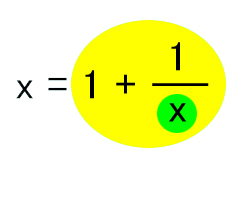
とあらわすことができます。（試しに緑の部分に黄色の部分を代入してみてください。）

これは、

x² - x - 1 = 0

の解です。これを解くと、x>0より、

x = ( 1 + √5 )/2

この値は黄金数と呼ばれていますが、1 : x は黄金比と呼ばれ、いたるところに姿を現す美しい比です。参照→フィボナッチ数

では、ここでもう少し例を挙げて連分数展開のアルゴリズムを確立していきましょう。

例題）　次の値を連分数展開をしなさい。

(1) 7/31　　(2) (2+√3)/3

(1)

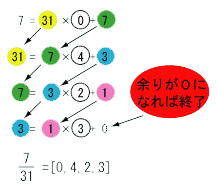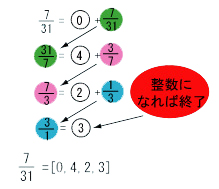上のどちらのやり方でもできますが、右の方がどちらかというと、単純ですかね。（右の方は矢印で逆数になります。）

(2)上の右のやり方で解きます。

(2+√3)/2 = 1 + (√3-1)/3　（１は整数部分）

3/(√3-1) = 3(√3+1)/2 = 4 + (3√3-5)/2　…(*)

2/(3√3-5) = 2(3√3+5)/2 = 3√3+5 = 10 + (3√3-5)

1/(3√3-5) = (3√3+5)/2 = 5 + (3√3-5)/2

ここで(*)の少数部分（下線部分）と一致しましたね。

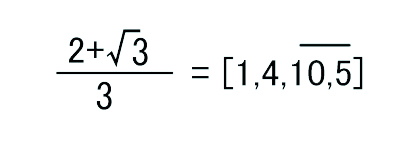
＜超越数の連分数展開＞

超越数である e やπの連分数展開はどうなるのでしょう？

ここでは、結果しか書きませんが、不思議な感じがします。

e = [2,1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,1,…]

π= [3,7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,2,2,…]

e に関しては規則性がありますが、πはなんの規則性もなさそうですね。

＜近似＞

いままで、無理数の無限連分数展開を扱ってきましたが、たとえば、次のような無限連分数があるとします。

α=[p₁,p₂,p₃,…,p_n,…]

このとき、

α≒[p₁,p₂,p₃,…,p_n]

と近似できるわけです。また、

α=[p₁,p₂,p₃,…,p_n] (n→∞)

ともあらわすことができます。

この方法で近似を行うことによって、無理数を有理数で近似できることになります。

　連分数(Continued Fraction)