フィボナッチ数(Fibonacci Numbers)
フィボナッチ数とは
理系出身の人なら一度は聞いたことがあるのではないでしょうか？
フィボナッチ数とは次のような数列（フィボナッチ数列）で示される値です。
（０、１、１、２、３、５、８、１３、２１、３４、…）
つまり初項 a1 = 0、第二項 a2 = 1 としてそれ以降は次の漸化式であらわされます。
an+2 = an+1 + an (n は自然数)
|
フィボナッチ数列
|
|
a1 = 0、a2 = 1 an+2 = an+1 + an (n は自然数) |
つまりある項が知りたければその手前の２つの数の和ででるわけなのですね。
フィボナッチ数列の一般項
ではその一般項を求めてみましょう。
an+2 = an+1 + an
を変形して
an+2 - αan+1 = β(an+1 - αan)
の形にすれば良かったですね。このとき
α、β = (1±√5)/2
なので
an+2 - (1＋√5)/2・an+1 = (1-√5)/2・(an+1 - (1＋√5)/2・an)
= {(1-√5)/2}n・(a2 - (1＋√5)/2・a1) = {(1-√5)/2}n …（１）
同様に
an+2 - (1-√5)/2・an+1 = {(1+√5)/2}n …（２）
（１）、（２）の辺々引き算すると
-√5 an+1 = {(1-√5)/2}n - {(1+√5)/2}n
√5an+1 = {(1+√5)/2}n - {(1-√5)/2}n
よってフィボナッチ数列の一般項は次のようになる。
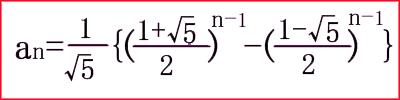
黄金比(Golden Section)
下に示す長方形は２辺の比が 1 : x (x > 1) で、この長方形から下図のように正方形をとります（赤い部分）。残った長方形の辺の比は 1 : x となり同様にして次々と正方形をとっていくと（青→緑→黄）、その残りの長方形の辺の比は常に 1 : x です。このときの x を求めてみましょう。
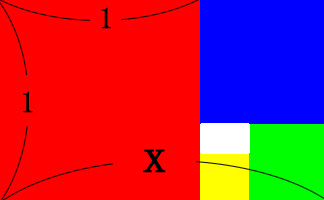
簡単にするために赤い正方形の一辺の長さを１とします。すると青の正方形の一辺は x - 1 です。残りの長方形の辺の比が 1 : x なので
x - 1 : 1 = 1 : x
x2 - x - 1 = 0
x = (1+√5)/2
この比を黄金比といいます。この値は先ほどフィボナッチ数列の一般項を求めるときにα、βの値としてでた数値です。
(1+√5)/2 = 1.618033989…
黄金比は自然対数の底 e や円周率πのように、自然界のいたるところで目にすることができます。
ちなみに私たちが日頃よく扱う紙の大きさＡ４、Ｂ５などや四つ切り、八つ切りなどの辺の比はだいたい 1 : √2 になってます。
