
 複素数(complex numbers)
複素数(complex numbers)
すべての実数は数直線上の一点としてあらわすことができました。複素数は当然数直線上にはすべてを表示することは不可能です。そのため複素数全体を視覚的にとらえるために考えられたのが複素平面(ガウス平面)です。
複素数 a は一般に次のようにあらわすことができます。
|
a = r cos θ + ir sin θ ( i は虚数単位: i2 = -1) |
ここで複素数 a の実数成分 r cos θ を実部、虚数成分 r sin θ を虚部とよびます。また r は複素数 a の絶対値とよび、r = | a | とあらわします。θ は a の偏角(位相)とよばれ θ = arg a とあらわし、0 <θs θ ≦ 2π なら偏角の主値とよばれ、Arg a とあらわします。
複素数 a を複素平面上であらわすと下のようになります。
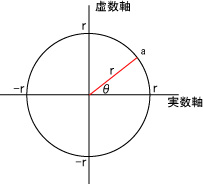
この複素平面上にすべての複素数は表示されることになります。
次に下に示されるような複素数 e(θ) を考えます。
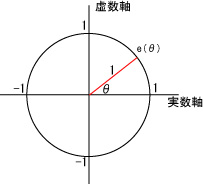
つまり
e(θ) = cos θ + i sin θ
となります。このとき a は
a = r e(θ)
とあらわすことができます。次のような図を考えます。
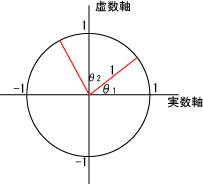
結局、この2つの複素数の合成は e(θ1 + θ2) とあらわすことができます。
e(θ1 + θ2) = cos (θ1 + θ2) + i sin (θ1 + θ2)
= cosθ1 cosθ2 - sinθ1 sinθ2 + i sinθ1 cosθ2 + i cosθ1 sinθ2
= cosθ1 (cosθ2 + i sinθ2) + sinθ1(-sinθ2 + i cosθ2)
= cosθ1 (cosθ2 + i sinθ2) + i sinθ1(cosθ2 + i sinθ2)
= ( cosθ1 + i sinθ1) (cosθ2 + i sinθ2)
= e(θ1) e(θ2)
よって次のことが成立する。
|
e(θ1 + θ2) = e(θ1) e(θ2)
|
この式を一般化すると
|
e(θ1 + θ2 + …+ θn) = e(θ1) e(θ2) … e(θn)
|
θ1 = θ2 = … = θn = θとおくと
e(nθ) = { e(θ)}n
従って次の公式が成り立つ。
|
ド・モアブルの公式
|
|
cos nθ + i sin nθ = (cos θ + i sin θ)n
|
次に e(θ) = cos θ + i sin θ をθで微分すると
de(θ)/dθ = d cos θ/dθ + i d sin θ/dθ
= -sin θ+ i cos θ
= i(cos θ + i sin θ)
= i e(θ)
e(0) = 1 より
de(θ)/dθ = i e(θ) 、e(0) = 1
の微分方程式を解くと関数e(θ)となる。
よって
e(θ) = eiθ
従って、次の公式が成り立つ。
|
eiθ = cos θ + i sin θ
|
ところでe(θ)が具体的にどのような関数なのかを考えます。
e(θ) = cos θ + i sin θ
= cos (θ + 2π) + i sin (θ + 2π)
であることは複素平面から明らかなので関数e(θ)は周期2πの周期関数です。またe(θ)の絶対値は常に1です。
