回帰曲線２次曲線および n 次曲線統計学入門

前章で２変量の直線回帰について考えましたが、この章では非直線回帰について考えていきます。

まずは、２次曲線による曲線回帰についてみていきます。

＜２次曲線による回帰＞

２次曲線の一般型として次の曲線から考えます。

y = ax² + bx + c ( = f(x) )

この曲線について最小２乗法を当てはめていきます。

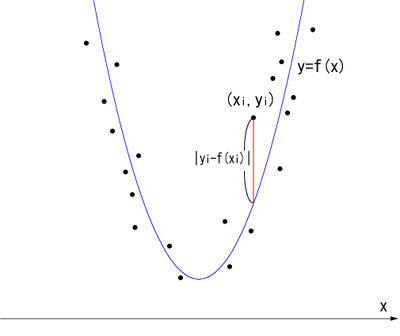
最小２乗法では赤い線分の長さ ( | y_i - f (x_i) | ) の２乗和の最小値を求めました。同様の方法でこの２次曲線の方程式を特定します。

この方法は３次曲線以上の回帰についても同様の方法で、曲線を特定することができます。