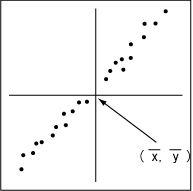
この図に表されている２変量は強い正の相関を示しています。このとき、すべての点がある直線上にあるとき、相関係数は１になります。

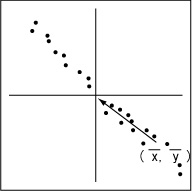
この図に表されている２変量は強い負の相関を示しています。このとき、すべての点がある直線上にあるとき、相関係数は -1 になります。

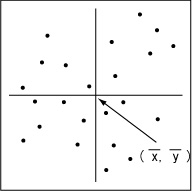
この図にあらわされる２変量の相関は見られません。

このように２変量に強い相関関係がみられるとき、それをよくあらわす直線が存在します。その直線について考えていきましょう。

　

＜回帰直線＞

下の図に示す２変量は強い相関が見られます。

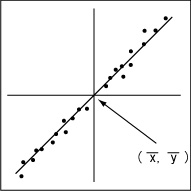
これらの点は、ある直線（回帰直線）で近似的にあらわされます。この直線の方程式が分かれば他のデータに関しても推測することが可能となるわけです。では、どのように回帰直線の方程式を出せばいいのでしょうか？回帰直線をあらわす関数を y = f(x) とします。このとき、関数 y = f(x) と平面上にプロットされた点P_i( x_i,y_i ) の関係は下の図のようになります。

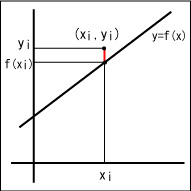
ここで点P_iのy軸方向の距離は赤い線分で示されます。この長さは

| y_i - f(x_i) |

となり、絶対値記号が付いているので、その２乗{ y_i - f(x_i) }² を考えます。

各点におけるこの値の和が、最小となる f(x) を定めるわけですね。この方法を最小２乗法(Least square method)と呼ばれています。

ここで、回帰直線の方程式を

y = a ( x - x~) + b 　　(　= f(x)　)

とおきます。x~はxの平均です。このとき、

L = Σ{ y_i - a( x_i - x~) - b }²

が最小となるa,bを求めていきます。これは、dL/da=0　と　dL/db=0　の連立方程式を解けばいいわけです。

dL/da = -2Σ( x_i - x~){ yi - a( x_i - x~) - b } = 0　　…(1)

dL/db = -2Σ{ y_i - a( x_i - x~) - b } = 0　　…(2)

(2)⇔Σ{ y_i - a( x_i - x~) - b } = 0

⇔Σy_i - aΣ( x_i - x~) - Σb = 0　（ここで両辺をnで割る。）

⇔ Σy_i/n - aΣ( x_i - x~)/n - 1/n・Σb = 0

⇔ y~ - aΣx_i/n + ax~ - b = 0

⇔ y~ - ax~ + ax~ - b = 0

⇔ b = y~

これを(1)に代入。

(1)⇔Σ( x_i - x~){ y_i - a( x_i - x~) - y~ } = 0

⇔ Σ( x_i - x~){ ( y_i - y~ ) - a( x_i - x~) } = 0

⇔ Σ( x_i - x~)( y_i - y~ ) - aΣ( x_i - x~)² = 0

⇔ a = Σ( x_i - x~)( y_i - y~ )/Σ( x_i - x~)²

⇔ a = （ x と y の共分散）/（ x の分散）²

以上より回帰直線の方程式は

y = Sxy/Sx²・( x - x~) + y~

となります。

回帰直線

y = Sxy/Sx2・( x - x~) + y~

　

＜なぜ回帰直線か？＞

回帰直線の名前の由来についてですが、普通に考えるとこのような名前を付けるのは些か不可解なように思います。これには、わけがあって、生物学者であり統計学者でもある（他に医学、心理学、人類学、社会学、教育学）ゴルトンFrancis Galton (1822-1911)によって付けられたものです。

彼は、身長の高い男達を集めてきて統計的に分析し、彼らの息子達の身長も同様に分析しました。すると、父親の代に比べて、息子達の身長の方が、より平均身長に近づいて行くことを発見しました。つまり平均と随分異なっていても、遺伝の結果、平均に戻っていく（回帰していく）ことを発見したわけです。