２つの母平均の差の検定
２つの母集団A,Bがある場合そのそれぞれの母平均の差があるかないかを検定する方法を示します。手順は次の通りです。
＜母分散が既知のとき＞
１．まずは、仮説を立てます。
帰無仮説：”２つの母平均μA,μBには差がない。”
対立仮説：”２つの母平均μA,μBには差がある。”
２．有意水準 α を決め、そのときの正規分布の値 k を正規分布表より得る。
３．検定統計量 T を計算。
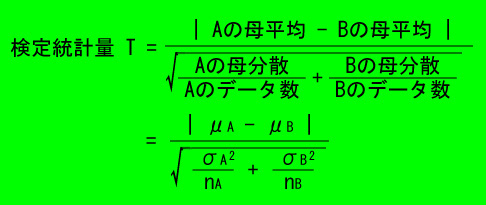
⇒ T＞k で帰無仮説を棄却し、対立仮説を採用。
＜母分散が未知のとき＞
母分散σA,σBが未知だが、σA = σB のときは t 検定を適用できます。
１．同様にまずは、仮説を立てます。
帰無仮説：”２つの母平均μA,μBには差がない。”
対立仮説：”２つの母平均μA,μBには差がある。”
２．有意水準 α を決め、そのときの t 分布の値 k （自由度 = nA + nB -2)を t 分布表より得る。
３．検定統計量 T を計算。
このときの分散σAB2は次のようにして計算します。
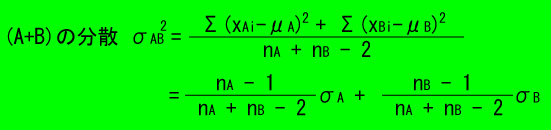
⇒ T＞k で帰無仮説を棄却し、対立仮説を採用。
２つの母平均の差の検定
