ケンドールの順位相関係数
ケンドールの順位相関係数
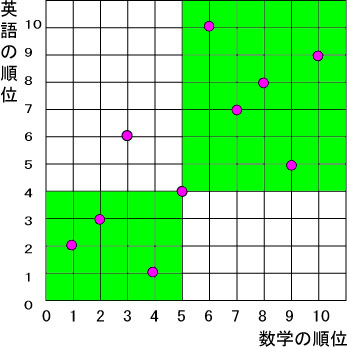
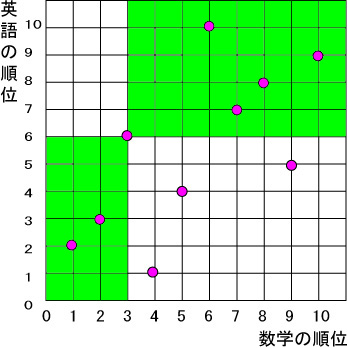
ケンドールの順位相関係数は、2変量の順位を座標平面上にプロットした際、ある一点より右上または左下にあるもの個数から、左上または右下にある点の個数を引いた数の和を n(n-1) で割ったものです。

|
例
|
|||||||||||||||||||||||||||||||||
10人の学生に数学と英語の試験を行ったところ、それぞれの順位は次の表のようになった。ケンドールの順位相関係数を計算して、それぞれの相関関係を調べよ。 |
|||||||||||||||||||||||||||||||||
各学生を座標平面上にプロットし、たとえば、3番目の学生を見てみますと、数学5番、英語4番です。この点より右上の点の個数は下図のように5点左下は3点、合計8点です。また、左上は1点、右下は0点、合計1点です。その差は 8-1=7点です。 |