スピアマンの順位相関係数

相関係数は２変量に直線的な相関関係があれば適用されるが、そうでない場合やデータの順位しか分かっていない場合もあります。そんなときに有効なのがスピアマンの順位相関係数です。求め方は、以下のようになります。下に示すような２変量に関して順位がついています。

　 Xの順位 Yの順位
1 x1 y1
2 x2 y2
3 x3 y3
4 x4 y4
5 x5 y5
6 x6 y6
7 x7 y7
8 x8 y8
9 x9 y9
10 x10 y10

この場合、X,Yそれぞれは順位が１番から１０番までです。そこで相関係数の公式を思い出すと、

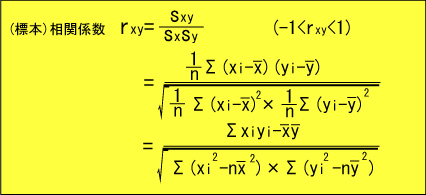
だったので、これをそのまま用います。ただし、

Σxi=Σyi=n(n+1)/2

Σxi2=Σyi2=n(n+1)(2n+1)/6

x~=y~=(n+1)/2

x~2=y~2=(n+1)2/4

です。このとき、相関係数を計算すると、

となります。相関係数の計算と何らかわらず、確率変数が順位になっただけのことです。

　

例
１０人の学生に数学と英語の試験を行ったところ、それぞれの順位は次の表のようになった。スピアマンの順位相関係数を計算して、それぞれの相関関係を調べよ。
学生 数学の順位 英語の順位
1 6 10
2 4 1
3 5 4
4 10 9
5 2 3
6 8 8
7 3 6
8 9 5
9 1 2
10 7 7
スピアマンの順位相関係数

= 1-6×Σ{(数学の順位)-(英語の順位)}2/{10×(102-1)}

= 1-6×{(-4)2+32+12+12+(-1)2+02+(-3)2+42+(-1)2+02}/990

= 0.703

となり、強い相関関係にあるといえる。つまり数学できるやつは英語もできる、数学できないやつは英語もできない。できるやつは何をやらしてもできる、できないやつは何をやらしてもできないという結果です。

　スピアマンの順位相関係数

TOP PAGE