独立性の検定(カイ2乗検定)
独立性の検定(カイ2乗検定)
2つの事象A,Bについて、独立かどうかを検定する方法を紹介します。まずは手順から…。
1.まずは、仮説から…。
帰無仮説:”2つの事象A,Bは独立である。”対立仮説:”2つの事象A,Bは独立でない。”
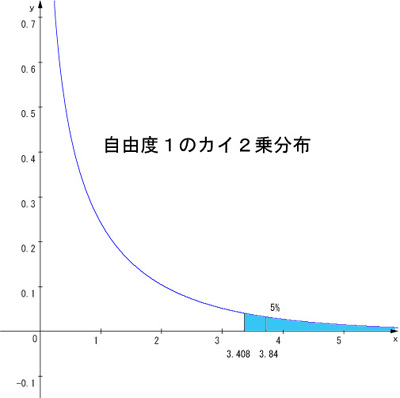
2.有意水準 α を決め、そのときのカイ2乗分布の値 k をカイ2乗分布表より得る。
3.データを表にする。
| 事象 | A1 | A2 | 合計 |
| B1 | A1B1 | A2B1 | SB1 |
| B2 | A1B2 | A2B2 | SB2 |
| 合計 | SA1 | SA2 | S |
4.検定統計量T(カイ2乗)を計算する。

⇒ T>k で帰無仮説を棄却し、対立仮説を採用。つまり、有意水準αで、2つの事象A,Bは独立でないといえます。
|
例
|
||||||||||||||||
新たに開発された狭心症の新薬を服用した人と、プラセボ(偽薬)を服用した人の5年間の発作が出現を表にすると次のようになった。 |
||||||||||||||||
まずは仮説をたてます。 |