＜ t 分布＞

正規分布は、母平均μと母分散σ²のみで示されたわけですが、一般にこれらの値は知られていない場合が多いようです。

そこで、母平均の代わりに標本平均で代用します。ここでは、この標本平均がどれほど母平均に近いかが問題となるわけです。

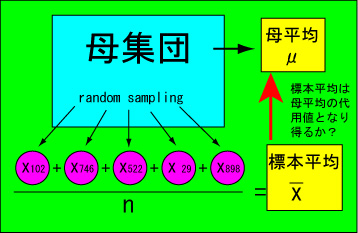
そこで、この標本平均x~はどのような分布を示すのでしょうか？

つまり、母集団の分布が下図のような正規分布N(μ,σ²)だとすると、

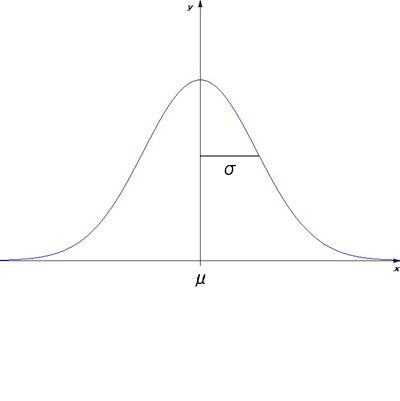
標本平均の分布は下図のような正規分布N(μ,σ²/n)となります。

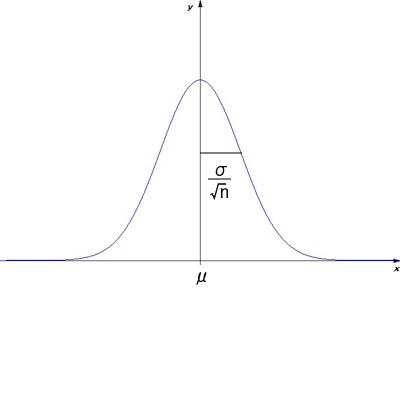
つまり、(x~-μ)/√(σ²/n) = (x~-μ)√n/σは正規分布N(0,1)を示します。

このように、標本平均が正規分布を示すには標本数が非常に多いということが前提となります。

標本数が少ない場合は、一般に上に示すような正規分布を示さないのです。では、標本数が少ない場合の標本平均はどのように評価すればいいのでしょうか？

標本数が少ない場合は、母標準偏差σの代わりに、

標本標準偏差 u_x (=√{1/(n-1)・Σ(xi-x~)²} )を用いて、

t = (x~-μ)√n/u_x = (x~-μ)√(n-1)/s_x

とおくと、t は平均０の t = 0 に関して対称な分布になります。

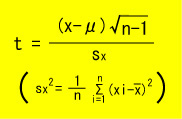
下図に示すように分布は正規分布によく似ていて、n=∞で正規分布となります。

　　

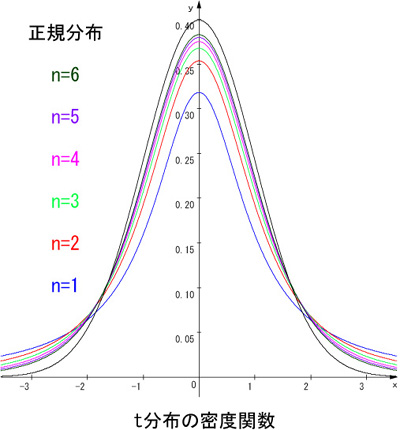
＜確率密度関数＞

t分布の密度関数は次のようになります。

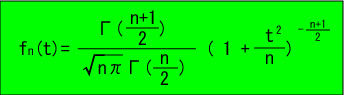ここでΓ(a)はガンマ関数と呼ばれ、次のように定義されます。

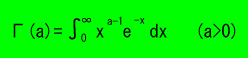このガンマ関数には次のような性質があります。

この性質を用いると

Γ(2) = 1! = 1

Γ(3) = 2! = 2

Γ(4) = 3! = 6

…

Γ(3/2) = 1/2×Γ(1/2) = (√π)/2

Γ(5/2) = 3/2×Γ(3/2) = (3√π)/4

Γ(7/2) = 5/2×Γ(5/2) = (15√π)/8

…

のように次々と要求されるガンマ関数の値が出てくるので、それらを使用して、

f₁(t)　= 1/{π(1+t²)}

f₂(t)　=　1/2√2　・　(1+t²/2)^-3/2

f₃(t)　=　2/π√3　・　(1+t²/3)^-2

f₄(t)　=　3/8　・　(1+t²/4)^-5/2

f₅(t)　=　8/π3√5　・　(1+t²/2)^-3/2

f₆(t)　=　15/16√6　・　(1+t²/6)^-7/2

…

のように計算して出すことが可能です。

＜コーシー分布＞

n = 1 のときの t 分布、

f₁(t)　= 1/{π(1+t²)}

は、とくにコーシー分布(Cauchy distribution)と呼ばれています。コーシー分布には平均が存在せず、その分布関数は、

F(x) = 1/2 + (tan^-1x)/π　　(-∞＜x＜∞)

となります。