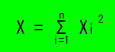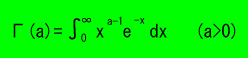カイ２乗分布

カイ２乗分布

確率変数 X1,X2,…,Xn は互いに独立でN(0,1)に従うものとする。このとき、 を自由度 n のカイ２乗分布という。

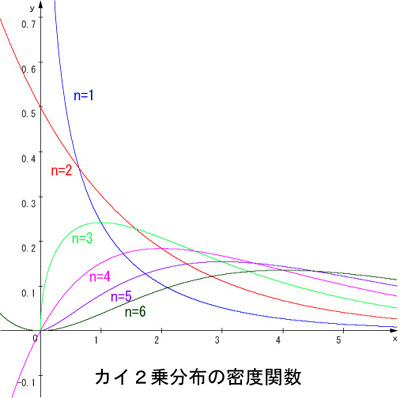
＜確率密度関数＞

カイ２乗分布の密度関数は次のようになります。

カイ２乗分布の密度関数

ここでΓ(a)はガンマ関数と呼ばれ、次のように定義されます。

ガンマ関数

このガンマ関数には次のような性質があります。

ガンマ関数の性質

Γ(a+1) = aΓ(a) Γ(1) = 1 Γ(1/2) = √π Γ(n+1) = n!　（ n は自然数）

この性質を用いると

Γ(2) = 1! = 1

Γ(3) = 2! = 2

Γ(4) = 3! = 6

…

Γ(3/2) = 1/2×Γ(1/2) = (√π)/2

Γ(5/2) = 3/2×Γ(3/2) = (3√π)/4

Γ(7/2) = 5/2×Γ(5/2) = (15√π)/8

…

のように次々と要求されるガンマ関数の値が出てくるので、それらを使用して、

f₁(x)　= 1/(2πxe^x)^1/2

f₂(x)　=　1/2　・　e^-x/2

f₃(x)　=　√(x/2π)　・　e^-x/2

f₄(x)　=　x/4　・　e^-x/2

f₅(x)　=　x^3/2/3√(2π)　・　e^-x/2

f₆(x)　=　x²/16　・　e^-x/2

…

のように計算して出すことが可能です。

　カイ２乗分布