正規分布1
正規分布1
2項分布で試行の回数を増やしていくと、ある一定の分布に近づいていきます。この分布を正規分布:Normal distribution(ガウス分布:Gaussian distribution)といいます。
B(10,0.5)、B(20,0.5)、B(30,0.5)の確率関数を見てみましょう。
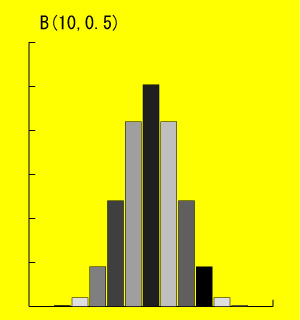
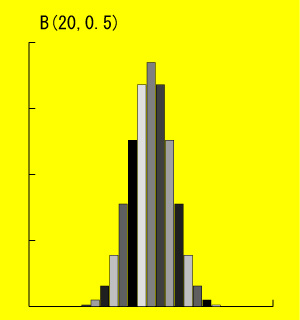
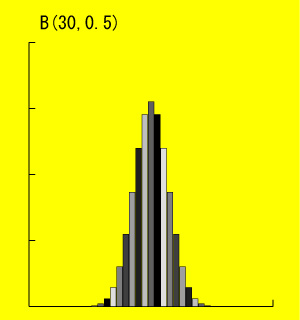
このように、n を大きくしていくと正規分布に近づいていきます。では正規分布とはどのような分布なのでしょうか?
|
正規分布
|
|
|
確率密度関数
|
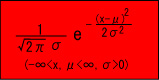 |
|
積率母関数
|
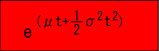 |
|
平均
|
μ
|
|
分散
|
σ2
|
確率密度関数が上に示すとおりなので、積率母関数Mx(t)は、
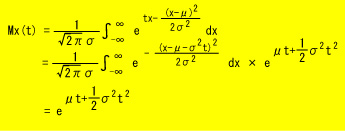
となり、このことから、平均はμ、分散はσ2となります。正規分布の密度関数をグラフにすると次のようになります。
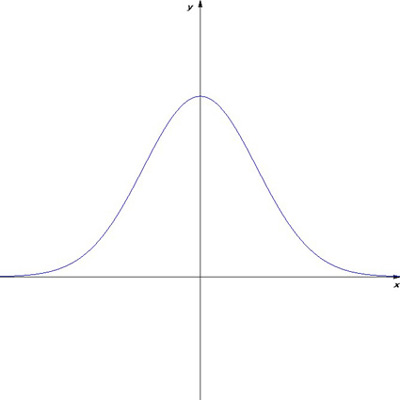
正規分布はドイツの大数学者ガウス(Johann Carl Friedrich Gauss, 1777-1855)によって発見されました。ガウスは、山の高さを計測するとき、毎回値が少しずつ異なりその誤差がこの正規分布に近づくことに気づきました。
では、密度関数が
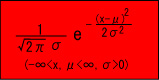
であらわさられる上のグラフはどのような性質を持ったものでしょうか?まあ頂点のときは x = μ となるのは容易に想像つきますが。
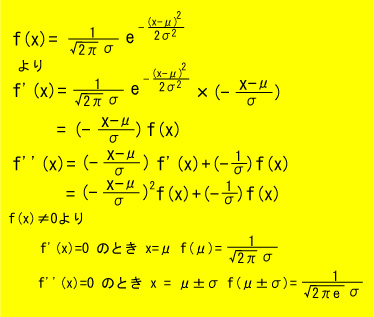
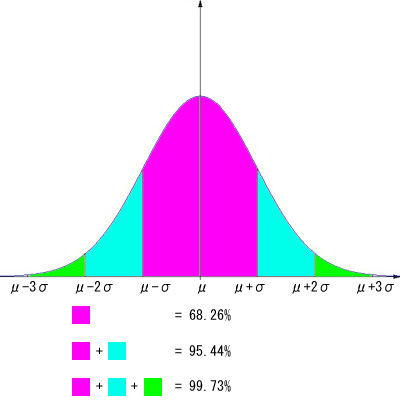
つまり下のようになるわけです。
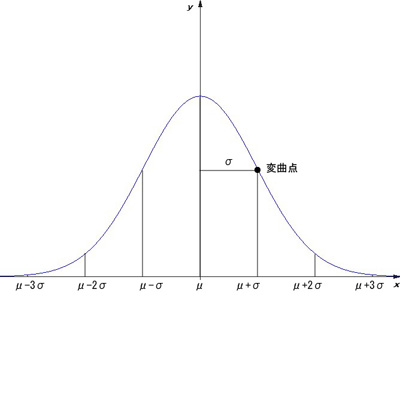
また、全体に対する μ-kσ≦x≦μ+kσ( k = 1,2,3)の部分の占める割合は下に示すようになります。