２項分布は、n が大きくなるほど、計算が非常に大変になってしまい、その場合は実用的とはいえません。そこで、p が小さいときに限り、近似式を応用して考えようとするのがポアソン分布(Poisson Distribution)です。

まず、２項分布B(n,p)の積率母関数は、

Mx(t) = ( pe^t + 1 - p )ⁿ

ここで平均E(X) = np = λとすると、

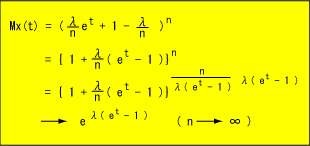
このときの確率関数を考えます。

Mx(t) = exp{λ( e^t - 1 )}

= e^-λ・exp(λe^t)

= e^-λΣ{(λe^t)^k/k!}

= Σe^tk・e^-λ(λ^k/k!)

∴p_k = e^-λ(λ^k/k!)