
 2変量への応用
2変量への応用
2変量のデータを取り扱うときに、そのデータを視覚的にとらえる方法として、相関図(散布図)や相関表があります。
相関図は2変量のデータをそのまま平面の座標としてとっていった図です(下図)。
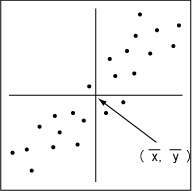
相関表は、度数分布表を2変量にそのまま応用した表です(下図)。
|
階級値
|
a1 | a2 | a3 | a4 | a5 | 計 |
| b1 | c11 | c12 | c13 | c14 | c15 | c1_ |
| b2 | c21 | c22 | c23 | c24 | c25 | c2_ |
| b3 | c31 | c32 | c33 | c34 | c35 | c3_ |
| b4 | c41 | c42 | c43 | c44 | c45 | c4_ |
|
b5
|
c51 | c52 | c53 | c54 | c55 | c5_ |
|
計
|
c_1 | c_2 | c_3 | c_4 | c_5 | n |
<共分散>
2変量のデータの相関関係を知る指標として次のものがあります。
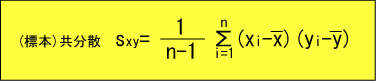
共分散の特徴として、
x が大きければ大きいほど y も大きく、
x が小さければ小さいほど y も小さい
とき、その値は大きくなります。
標本共分散に対して母共分散は、x,yの母平均をそれぞれμx,μyとして次のようになります。
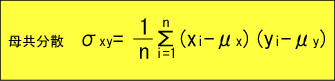
この母共分散は次のように変形することができます。
σxy = 1/n・Σ( xi - x~ )( yi - y~ )
= 1/n・Σ( xiyi - x~yi - y~xi + x~y~ )
= 1/n・Σxiyi - x~・Σyi/n - y~・Σxi/n + Σx~y~/n
= 1/n・Σxiyi - x~・y~ - y~・x~ + nx~y~/n
= 1/n・Σxiyi - x~・y~ - y~・x~ + nx~y~/n
= 1/n・Σxiyi - x~・y~
<相関係数>
また共分散の他に、
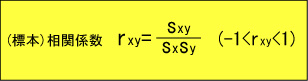
もよく使用される指標です。共分散はその値がデータの単位によって代わる性質がありますが、相関係数は単位によらず一定値となります。
