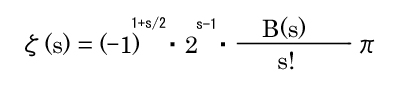ゼータ関数 (Riemann Zeta Function)
オイラの前振り
素数のページでもふれているように、素数は無限に存在するので当然、素数の和が無限大になるのは直感的に理解いただけるでしょう。
しかし、素数の逆数の和は？というと直感だけではなかなか分からないはずです。
素数の和が無限大なのだから当然、逆数の和も無限大になるという考えは無理がありすぎます。下の例で考えてみましょう。
（２、４、８、１６、…、２ｎ、…） …（＊）
この数列は初項２、項比２の数列であり、この和
S1 = 2 + 4 + 8 + 16 + …
は明らかに無限大になります（証明略）。
しかしその逆数の和はどうなるでしょう。
S2 = 1/2 + 1/4 + 1/8 + 1/16 + …
これは初項1/2、項比1/2の無限等比級数です。
S2 = limΣ(1/2)n
= lim{1/2×(1-1/2n)}/(1-1/2)
= lim(1 - 1/2n)
→ 1 (n → ∞)
つまり数列（＊）の和は無限大でしたけど、その逆数の和は１に収束するってなわけです。
自然数の逆数の和はどうでしょうか？
T1 = 1/1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + 1/9 + 1/10 + 1/11 + 1/12 + 1/13 + 1/14 + 1/15 + 1/16 + …
= 1/1 + 1/2 + (1/3 + 1/4) + (1/5 + 1/6 + 1/7 + 1/8) + (1/9 + 1/10 + 1/11 + 1/12 + 1/13 + 1/14 + 1/15 + 1/16) + …
T2 = 1/1 + 1/2 + (1/4 + 1/4) + (1/8 + 1/8 + 1/8 + 1/8) + (1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16) + …
= 1 + 1/2 + 1/2 + 1/2 + 1/2 + …
→∞
T1 > T2 で T2 → ∞ なので T2 → ∞ となります。つまり自然数の逆数の和は、無限大。
では、話を戻して素数の逆数の和はどうでしょう。あ、やっぱり、戻すのやめ。もう少し前振りを続けましょう。
オイラーの前振り
まず無限等比級数の公式を思い出してください。
-1<x<1のとき初項１、項比 x の無限等比級数は
Σ xn = 1/(1 - x)
となりました。
ここで x に素数の逆数を入れていくと
1/(1-1/2) = 1/20 + 1/21 + 1/22 + 1/23 + 1/24 + …
1/(1-1/3) = 1/30 + 1/31 + 1/32 + 1/33 + 1/34 + …
1/(1-1/5) = 1/50 + 1/51 + 1/52 + 1/53 + 1/54 + …
1/(1-1/7) = 1/70 + 1/71 + 1/72 + 1/73 + 1/74 + …
のようになります。これらを辺々かけあわせると、
1/(1-1/2) × 1/(1-1/3) × 1/(1-1/5) × 1/(1-1/7) × …
= (1/20 + 1/21 + 1/22 + 1/23 + 1/24 + …) × (1/30 + 1/31 + 1/32 + 1/33 + 1/34 + …) ×
(1/50 + 1/51 + 1/52 + 1/53 + 1/54 + …) × (1/70 + 1/71 + 1/72 + 1/73 + 1/74 + …) × …
となります。ここで右辺を展開すると、
1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + 1/9 + …
となり、これは自然数の逆数の和です。
これは無限大になりましたね。つまり
U = 1/(1-1/2) × 1/(1-1/3) × 1/(1-1/5) × 1/(1-1/7) × … = ∞
なんですね。ここでオイラーが使用した公式は
0 ＜ x ≦ 1/2 のとき
1/( 1 - x ) ≦ 10x
です。これを利用すると、
U = 1/(1-1/2) × 1/(1-1/3) × 1/(1-1/5) × 1/(1-1/7) × …
≦ 101/2+1/3+1/5+1/7+…
Uは無限大なのでそれより大きい
101/2+1/3+1/5+1/7+…
も無限大となり、
1/2 + 1/3 + 1/5 + 1/7 + …
つまり素数の逆数の和も無限大になるわけです。
オイラー積
オイラー積とは p をすべての素数として
Π 1/(1-1/ps) = 1/(1-1/2s) × 1/(1-1/3s) × 1/(1-1/5s) × 1/(1-1/7s) × …
であらわされるものです。オイラー積も先の例に従って
Π 1/(1-1/ps) = 1/1s + 1/2s + 1/3s + 1/4s + 1/5s + 1/6s +…
となりますね。
（この項目の入力ミスを高木様がご指摘くださいました。高木様ありがとうございました。）
ゼータ関数
ゼータ関数とは
ζ(s) = 1/1s + 1/2s + 1/3s + 1/4s + 1/5s + 1/6s + …
= Σ1/xs
で定義されます。
つまり
ζ(s) = Σ 1/xs = Π 1/(1-1/ps)
なのです。
ベルヌーイ数
高等学校の数学で習った、次のような公式を思い出してください。
Σ k = n(n + 1)/2
Σ k2 = n ( n + 1 ) ( 2n + 1 )/6
Σ k3 = {n(n + 1)/2}2
( k = 1、2、3、…、n)
これらはたしか、教科書にも公式として出ていたような気がします。昔のことなので忘れました。
このような公式を見ると、多少数学に興味がある人なら一般化したくなるのが普通ですよね。
この公式を一般化したのが次の式です。
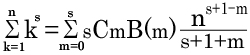
ここでB(m)とは次の漸化式であらわされる定数です。
…（＊＊）
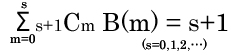このB(m)がベルヌーイ数です。
具体的にB(m)の値を出してみましょう。
まず s = 0 として（＊＊）は
B(0) = 1
また s = 1 のとき
B(0) + 2B(1) = 2
B(1) = 1/2
となりますね。n = 2のとき２ のとき
B(0) + 3B(1) + 3B(2) = 3
∴B(2) = 1/6
同様に n = 3 のとき
B(0) + 4B(1) + 6B(2) + 4B(3) = 4
∴B(3) = 0
n = 4 のとき
B(0) + 5B(1) + 10B(2) + 10B(3) + 5B(4) = 5
∴B(4) = -1/30
このように漸化式を次々に解いていくと
|
m
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
|
B(m)
|
1
|
1/2
|
1/6
|
0
|
-1/30
|
0
|
1/42
|
0
|
-1/30
|
0
|
5/66
|
0
|
-691/2730
|
0
|
7/6
|
のようになります。
では、具体的にζ(2)、ζ(3)などは、どのような数値になるのでしょうか？
ゼータの値
ここで思い出していただきたいのがマクローリン展開です。
sin x をマクローリン展開しますと、
sin x = x - x3/3! + x5/5! - x7/7! + x9/9! - … …（＊＊＊）
となりました。
また sin x は kπ(kは整数) を解に持つので次のように、無限積展開されます。
sin x = x Π (1 - x/kπ)
= … (1 + x/3) (1 + x/2) (1 + x) x (1 - x) (1 - x/2) (1 - x/3) …
= x (1 - x2/π2)(1 - x2/22π2)(1 - x2/32π2) …
= x Π (1 - x2/k2π2)
これを展開すると
sin x = x - 1/π2×(1/12 + 1/22 + 1/32 + 1/42 + …)x3 - 1/π5(なんとか) x5 + …となり（＊＊＊）と係数を比較すると
ζ(2) = 1/12 + 1/22 + 1/32 + 1/42 + … = π2/6
ζ(3)の値もきれいに書きたいところだけど無理。というか無理数だったらしいことが1970年代後半にフランスのアベリにより示されました。ζ(3)どころか奇数は無理なんです。はい。
偶数はですねえ、次の表に示します。
|
ζ(2)
|
ζ(4)
|
ζ(6)
|
|
π2/(2×3)
|
π4/(2×32×5)
|
π6/(33×5×7)
|
|
ζ(8)
|
ζ(10)
|
ζ(12)
|
|
π8/(2×33×52×7)
|
π10/(35×52×7×11) |
π12/(36×53×72×11×13)
|
偶数の場合のゼータの値は次の一般式できれいに表されます。
