
 RSA暗号
RSA暗号
<従来の暗号>
これまでの暗号はすべて秘密鍵暗号で、暗号鍵と復号鍵が同一のものでした。つまり、暗号化関数 f でメッセージを暗号化すると、復号するときはその逆関数、f-1 で復号化するというものだったのです。
平文 --- f --→ 暗号文 --- f-1 --→ 平文
この場合、当事者間で、鍵をあらかじめ取り決めておかなくてはなりません。ここで問題なのは、隣に住んでいる人に、鍵を教えるのは容易でしょう。しかし、外国に住んでいる友人には、どのような手段で鍵を渡せばいいのでしょうか?実際、戦時中などは、その情報の極秘性故に、暗号文で通信が行われていたわけですが、鍵の配送には莫大な金がかかったと言われています。
”鍵ごと、メールや電話でやりとりしたいいのでは?”
と、思われる方もいるかもしれません。いないか?
しかし、そのメールや電話も第三者に読まれる可能性があるという点で、不可能なのです。
どれほど複雑なアルゴリズムを考えたところで、鍵を盗まれると解読は容易なものなのです。このこれまでの、秘密鍵暗号という概念とはまったく別の暗号システムが1970年代に登場しました。
<公開鍵暗号の登場>
1975年、スタンフォード大学の、ホイットフィールド・ディフィー(Whitfield Diffie)、マーティン・ヘルマン(Martin Hellman)、ラルフ・マークル(Ralph Merkle)らは、まったく新しい、暗号システムを発表しました。それは次のようなものでした。
AからBにメッセージを送りたいとします。A、Bそれぞれは個人鍵と公開鍵の2種類の鍵を持っているものとします。個人鍵は秘密にされているものであってAの個人鍵はAしか知りませんし、Bの個人鍵はBしか知りません。公開鍵はすべての人が知り得ることができるようになっています。まずAは、まずはじめにメッセージをBの公開鍵を使用して暗号化します。これを受信した、BはBの個人鍵を使用して復号化するということです。
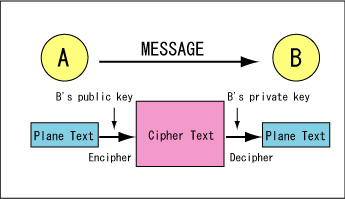
つまり、暗号化と複合化では鍵が違っているわけです。暗号鍵で暗号化されたメッセージは暗号鍵では復号されないのです。この方法では、従来の逆関数が存在する関数(双方向関数)ではあり得ないことのように思えます。ホイットフィールド・ディフィーらはこの画期的な方法を発見しましたが、実用されるような一方向関数のアルゴリズムまでは発見していないようです。
<RSAの登場>
実用可能な一方向関数は1977年、マサチューセッツ工科大学(MIT)のレナード・アドルマン(Leonard Adleman)、ロン・リヴェスト(Ron Rivest)、アディ・シャミア(Adi Shamir) らによって発表されました。それは素因数分解の一意性というものを利用しています。(素数に関して)
実用化されたこのアルゴリズムは彼らの名前の頭文字をとって、RSAと名付けられました。
RSA Security社によればそのアルゴリズムは以下のようなものです。
AがBにメッセージを送るものとします。まずBは充分に大きな素数を p、q 2種類用意します。
n = p×q
とします。次にBは ( p - 1 ) ( q - 1 ) と互いに素な n より小さい数 e を用意します。この n、e は公開鍵です。またBは
e×d ≡ 1 (mod (p-1)(q-1))
より d を計算します。d はBの個人鍵です。ここでAはBの公開鍵 n、e を使って、メッセージMを次の式で暗号文C:Cipherに暗号化します。
C ≡ Me( mod n)
Cを受け取ったBは、Bの個人鍵 d を用いて、
M ≡ Cd(mod (p-1)(q-1))
より元のメッセージMを得るというわけです。
このように、RSAアルゴリズムの安全性は、素因数分解することは難しいという仮定に基づいています。
2つの素数7687、9689からその積
7687×9689 = 74479343
を得るのは容易であるが、2つの素数の積、74479343から 7687×9689を得るのは困難なことなのです。実際にはもっと大きな素数が使用されています。そのため素因数分解の簡単な方法が発見されると、RSAは終焉を迎えることになるでしょう。
