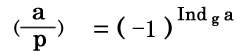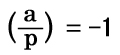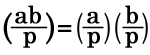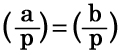平方剰余 (Quadratic Residue)
奇素数 p に関する２次合同式を
|
(a,p) = 1 として、 x2 ≡ a ( mod p ) …(*) が解を持つ。 |
とおくと、(*) が解を持つための必要十分条件は、
2Indgx ≡ Indga ( mod p-1 )
が解を持つことになります。このとき、2|p-1 より、
(*) ⇔ 2|Indga
ここで、ルジャンドルの記号を導入します。
|
ルジャンドルの記号（平方剰余記号）
|
|
(a,p) = 1 のとき、
|
この値は、
|
(*) が解を持てば、
となり、”a を mod p の平方剰余(quadratic residue)” といいます。 また、(*) が解を持たなければ、
となり、”a を mod p の 平方非剰余(quadratic non-residue)”といいます。 |
これには、次のような性質があります。
|
定理
|
|
|
(a,p) = 1 ならば、
|
|
|
a ≡ b (mod p)、(a,p) = (b,p) = 1 ならば、
|
|
|
オイラー基準
|
 |
|
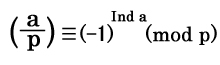第１補充法則
|
 |
|
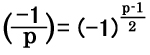第２補充法則
|
 |
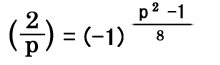| 平方剰余の相互法則 |
 |
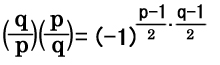＜ヤコビ記号＞
１より大きい（３以上の）奇数 n を次のように素因数分解する。
n = p1・p2・p3・ …
また、(m,n) = 1 とするとき、
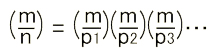
と定義し、左辺の記号をヤコビ記号 (Jacobi symbol) という。
|
定理
|
|
| m ≡ m' ( mod n ) ならば、 |  |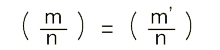
 |
|
|
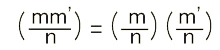m、n を１より大きな奇数とすると、
|
 |
 |
|
 |
|
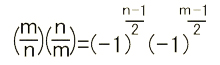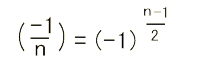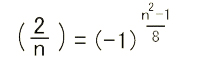*平方剰余の相互法則に誤りがありました。AA氏よりご指摘がありました。ありがとうございました。
