素数定理 (Prime Number Theorem)
１から自然数 n までの素数の個数を π(n) であらわします。そのとき π(n) を n を用いてあらわします。これはドイツの大数学者ガウス(Johann Carl Friedrich Gauss:1777-1855)によって、彼が１５歳の時に予想されたものです。
|
素数定理
|
 |
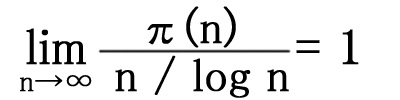つまり、１から自然数 n までの素数の個数は n が大きいほど n / log n に近づくということですね。
この定理は、１８９６年にアダマール(Hadamard, Jacques)とプーサン(Vall`ee Poussin)によってそれぞれ独立に証明されました。
では、実際に n に具体的な数値を代入して素数の個数がどれほどまでに n / log n に近づくか実験してみます。
|
n
|
個数
|
π(n)
|
|
10
|
4
|
4.3
|
|
100
|
25
|
21.7
|
|
1,000
|
168
|
144.8
|
|
10,000
|
1,229
|
1085.7
|
|
100,000
|
9,592
|
8685.9
|
|
1,000,000
|
78,498
|
72382.4
|
|
10,000,000
|
664,579
|
620420.7
|
|
100,000,000
|
5,761,455
|
5428681.0
|
|
1,000,000,000
|
50,847,534
|
48254942.4
|
|
10,000,000,000
|
455,052,511
|
434294481.9
|
|
100,000,000,000
|
4118,054,813
|
3948131654
|
いかがなものでしょうか？
