
 n 角数 (Numbers of n-angle)
n 角数 (Numbers of n-angle)
ここでは、n 角数について考えていきます。n 角数とはどういうものか、まずは3角数について考えます。
<3角数 (Triangular Number)>
三角数とは次のような数列であらわされる数のことです。
P3 : 1、3、6、10、15、21、28、…
勘のいい人はこの数列を見ただけで、
一般項 P3k = { k ( k + 1 ) }/2
が思い浮かぶことでしょう。この数列の図形的に眺めてみますと、下の図のようになります。

左下の黄色い点から始まって、次に黄緑色の2点を含んだ合計3点の3角形、さらに緑の3点を含んだ合計6点の3角形、さらに水色の4点を含んだ合計10点の3角形…、と続いていきます。つまり、一辺が k の正三角形に含まれる点の数を数えたことになりますね。
<4角数 (Square Number)>
3角数同様、4角数についても考えていきましょう。下の図を見てください。

うーん。この一般項も簡単ですねえ。数列は次のような平方数になります。
P4 : 1、4、9、16、25、36、49、…
一般項 P4k = k2
3角数なら、一辺が k の正三角性を考えましたけど、4角数の場合は、一辺が k の正方形を考えればいいわけですね。
同様にして、5角数(Pentagonal Number)、6角数(Hexagonal Number)、7角数(Heptagonal Number)、8角数(Octagonal Number)、9角数(Nonagonal Number)、10角数(Decagonal Number)なども定義されます。しかし、いちいち一つずつ一般項を求めていくのは面倒くさいですね。次に n 角数の一般項を求めていきましょう。
<n 角数>
これもそれほど難しくはないですけど、今までほど単純ではないですね。早速、下の図を見ていきましょう。
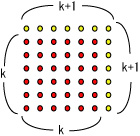
これは正方形で示されていますけど、正n角形と考えてください。まず一辺が k の正n角形の点の個数をPnkとします(図の赤い点の個数)。それに黄色い点の個数を加えたものをPnk+1として漸化式をつくりましょう。
Pnk+1 = Pnk + (黄色い点の個数)
となりますね。では黄色い点の個数を数えましょう。上の図のように正方形なら、黄色い点の個数は
k × 2 + 1
となりますけど、n角形の場合はどうなるのでしょう。答えは、簡単、
k × ( n - 2 ) + 1
となります。
∴ Pnk+1 = Pnk + { k × ( n - 2 ) + 1 }
これで漸化式が完成しました。あとはこの漸化式を解くだけです。これも易しいですね。
Pnk+1 - Pnk = { k × ( n - 2 ) + 1 }
と変形します。すると、
Pnk+1 - Pnk = { k × ( n - 2 ) + 1 }
Pnk - Pnk-1 = { (k-1) × ( n - 2 ) + 1 }
Pnk-1 - Pnk-2 = { (k-2) × ( n - 2 ) + 1 }
…
Pn3 - Pn2 = { 2 × ( n - 2 ) + 1 }
Pn2 - Pn1 = { 1 × ( n - 2 ) + 1 }
となりまして、辺々をすべてたすと、
Pnk+1 - Pn1 = Σ{ k × ( n - 2 ) + 1 }
となります。Pn1は常に1なので、
Pnk+1 = Σ{ k × ( n - 2 ) + 1 } + 1
となりあとは単純な計算ですね。
Pnk+1 = ( n - 2 ) Σk + k + 1
= ( n - 2 ) k ( k + 1 )/2 + ( k + 1 )
∴ Pnk = ( n - 2 ) k ( k - 1 )/2 + k
続く
