
 メビウス関数 (Mobius function)
メビウス関数 (Mobius function)
メビウス(August Ferdinand Mobius:1790-1868)といえば、おそらく多くの人が、”メビウスの輪”をすぐに思いつくことでしょう。ここでとりあげるのは、メビウス関数 (Mobius function)というものです。
|
メビウス関数 (Mobius function)
|
| メビウス関数μ(n)は次のように定義されます。
|
この場合、平方数には1を含みません。
このように定義されたメビウス関数について、次のようなことがいえます。
|
メビウスの反転公式(Inversion Formulas) |
|
f (n) = Σd|ng (d) ⇔ g (n) = Σd|nμ(d) f (n/d) ( = Σd|nμ(n/d) f (d) )
|
証明は後回しにして、 n に具体的な数を代入してみましょう。
例) n = 6 のとき
f (6) = Σd|6 g (d) = g (1) + g (2) + g (3) + g (6)
f (3) = Σd|3 g (d) = g (1) + g (3)
f (2) = Σd|2 g (d) = g (1) + g (2)
f (1) = Σd|1 g (d) = g (1)
となるので、g (1)、g (2)、g (3)、g (6)について解くと、
g (6) = f (1) - f (2) - f (3) + f (6)
g (3) = -f (1) + f (3)
g (2) = -f (1) + f (2)
g (1) = f (1)
これを利用して、
Σd|6μ(d) f (6/d) = μ(1) f (6/1) + μ(2) f (6/2) + μ(3) f (6/3) + μ(6) f (6/6)
= f (1) - f (2) - f (3) + f (6)
= g (6)
となるので、確かに n = 6 のときは反転公式は正しそうです。
では次に、この反転公式を証明してみましょう。
<メビウス関数は乗法的>
(a,b) = 1
とする。
(1) a または b 、または両方が平方数で割り切れるとすると、μ(a)とμ(b)の少なくとも一方は、0になるので、
μ(a)μ(b) = μ(ab) = 0
(2) a および b が平方数で割り切れないとすると、μ(a)とμ(b)はそれぞれ次のような異なる素数の積としてあらわされます。
μ(a) = p1p2p3…pm
μ(b) = q1q2q3…qn
(a,b) = 1 より、{ p1、p2、p3、…、pm、q1、q2、q3、…、qn }の( m + n )個の素数はすべて異なることになります。
∴μ(ab) = (-1)m+n
μ(a) = (-1)m、μ(b) = (-1)nより、
μ(a)μ(b) = μ(ab)
となります。
これで、メビウス関数μ(n)に関して、
”(a,b) = 1 なら、μ(a)μ(b) = μ(ab) ”(乗法的)が示されました。
| メビウス関数μ(n)は乗法的である。すなわち、
(a,b) = 1 なら、μ(a)μ(b) = μ(ab) が成り立つ。 |
<Σd|nμ(d) = e(n)>
e(n)とは、次のような関数です。
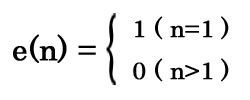 |
このとき、次のことが成立します。
|
Σd|nμ(d) = e(n)
|
証明は簡単。
(証明)
n = 1 のとき
Σd|1μ(d) = μ(1) = 1 = e(1)
n > 1 のとき
n = p1a1p2a2p3a3…pnan (p1p2p3…pnは素数)
と書くと、n の約数 d の中で、平方数で割り切れる数は、μ(d) = 0 となるので、Σd|nμ(d)を考えるとき、a1a2a3…anのそれぞれは、0または1のときを考えれば充分である。
Σd|nμ(d) = Σd|mμ(d) ( m = p1p2p3…pn)
= μ(0個の素数の積)の和 + μ(1個の素数の積)の和+μ(2個の素数の積)の和+μ(3個の素数の積)の和+ …+μ(n個の素数の積)の和
= 1 + (-1)1×nC1 + (-1)2×nC2 + (-1)3×nC3 + …+ (-1)n×nCn
= 0
(∵二項定理( a + b )n = ΣnCk ak bn-k (k:0→n)で a=-1、b=1 を代入。)
以上よりΣd|nμ(d) = e(n)は成立。
(証明終)
<メビウス関数は可換環>
メビウス関数に限らず、数論的関数はすべて可換環です。ここではその理由は触れません。また、可換環の定義もここでは触れません。
メビウスの反転公式
f (n) = Σd|ng (d) ⇔ g (n) = Σd|nμ(d) f (n/d) ( = Σd|nμ(n/d) f (d) )
をディリクレ積 * を用いてあらわすと、
f = g * μ-1 ⇔ g = f * μ
となります。(∵μ-1(n)=1)
これなら証明は簡単そうです。
f = g * μ-1
⇔ f * μ= g * μ-1 * μ
⇔ g = f * μ
(証明終)
簡単でしたね。
続く

