
 フェルマーの最終定理 (Fermat's last theorem)
フェルマーの最終定理 (Fermat's last theorem)
<フェルマーの最終定理とは>
| ( n = 3、4、5、6、…)に対して
xn + yn = zn を満たす自然数解(x、y、z)は存在しない。…(*) |
有名なフェルマーの最終定理 (Fermat's last theorem)ですね。単純ですね。小学生にも理解できそうです。あまりにも有名なので数学にふれる機会のない人も聞いたことあるかもしれませんね。
この定理は(定理になったのは最近の話、後述)1630年代フランス人ピエール・ド・フェルマー(Pierre de Fermat 1601-1665)がディオファントスの”算術”の第2巻問題8の余白に示したもので、証明は記述されていません。あの有名な
”この証明を記すにはこの余白はあまりに狭すぎる。”
とのことです。この余白が狭すぎたばっかりに、360年間も世界の数学者やアマチュア数学者を悩ませたのです。1995年2月13日にプリンストン大学のワイルズ(Andrew J. Wiles)が完全に証明し、(フェルマーの中では360年前からおそらく定理でしたが)”予想”が”定理”になったのは記憶に新しい話ですね。ワイルズは少年時代よりフェルマーの最終定理にふれ、数学への道を志したのですから、この問題は優れた数学者を輩出したといえます。また世界中の多くのアマチュア数学者に夢を与えました。そう考えるとディオファントスの”算術”に充分な余白があったり、フェルマーが思いついたことをメモじゃなく、すぐに論文にするようなら、状況は変わっていたかもしれません。少年時代のワイルズの目に入ってこなかったかもしれません。そういう意味でもこの定理は”大定理”であるとおもいます、わたしは、、、。
では、ワイルズが証明するまでの360年間のいきさつを順に考えていきましょう。
まず、(*)で = a d
xa + ya = za …(1)
が自然数解(x、y、z)が存在しないと仮定します。
すると、b を2以上の整数とすると、
(xb)a + (yb)a = (zb)a
は、(1)の特別な場合と考えることができて、
n = ab
のときも自然数解(x、y、z)が存在しないといえます。つまり、(*)を示すには、4とすべての奇素数について示せばいいことになりますね。
<オイラー予想>
1778年、オイラー(Leonhard Euler 1707-1783)はフェルマーの最終定理を次のように拡張しました。
|
オイラー予想
|
| ( n = 3、4、5、6、…)に対して、任意の自然数のn 乗である整数を、n 個より少ないn 乗数であらわすことができない。 |
これはつまり、
( n = 3、4、5、6、…)に対して
x1n + x2n + x3n + … + x(n-1)n= zn
を満たす自然数解(x1n、x2n 、x3n、…、x(n-1)、z)は存在しない。
ということです。
もしこの予想が正しければ、フェルマーの最終定理も正しいことになりますね。この予想も証明されないまま、200年近くの年月が過ぎました。しかし、コンピュータの発展はこの予想に終止符を打ちました。
1966年にLander と Parkin が、
275 + 845 + 1105 + 1335 = 1445
そして、1988年には Elkies とFryetは、
958004 + 2175194 + 4145604 = 4224814
を発見したのです。つまり反例を見つけたわけです。
<n = 3 のとき>
オイラー予想は残念ながら、定理にはならなかったのですが、n = 3 のとき(*)が成り立つことを示したのも、オイラーでした。
続く
<n = 4 のとき>
x2 + y2 = z2 …(*1)
の整数解は、中学校で三平方の定理を習ったときいくつか出てきて、また無限に存在することも習いました。では、このような形であらわされる整数解はどのような形をしているのでしょうか?これは高校で積分を扱ったときに変数変換を行った際に実は出てきていたのです(後述)。
ここで、(x,y,z) = 1 とします。なぜなら、(x,y,z) = s (s ≠ 1)としますと、
(*1)⇔(sx')2 + (sy')2 = (sz')2
⇔s2x'2 + s2y'2 = s2z'2
つまりx'2 + y'2 = z'2 (x',y',z') = 1の整数解がでてこれば、その両辺に平方数をかけることによりいくらでも整数解が得られることになります。したがって、(x,y,z) = 1 とします。
まず x,y,z のそれぞれの偶奇を考えてみましょう。
|
x,y の両方が偶数のとき |
z も偶数になり、これは(x,y,z) = 1 に反します。 |
|
片方が偶数、もう片方が奇数のとき |
ありえます。 |
|
x,y の両方が奇数のとき |
奇数の平方は奇数であり、2つの奇数の和は偶数なので、z は偶数となり、
x = 2m+1、y = 2n+1 とおくと、
よってこれもあり得ない。 |
よって、片方が偶数、もう片方が奇数となる。ここで、x を偶数、y を奇数として差し支えありません。(もちろん、z は奇数です)
そのとき、
|
(x,y,z) = (2ab,a2-b2,a2+b2) |
つまり、
|
としてあらわせます。
イメージ的には…
まず、下のような単位円を考えてください。
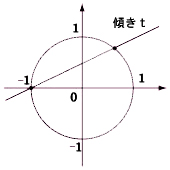
(-1,0)を通り、傾き t の直線の方程式は、
y = t(x+1)
で与えられます。この直線と、単位円との(-1,0)以外の交点を求めると、
x2 + y2 = 1
との連立方程式を解いて、
((1-t2)/(1+t2),2t/(1+t2))
これは、
{(1-t2)/(1+t2)}2 + {2t/(1+t2)}2 = 1
なので、
(1-t2)2 + (2t)2 = (1+t2)2
この t に整数値を代入することによって、(*1)の整数解が得られます。
これを
x4 + y4 = z2
のときで考えると、
|
(x2,y2,z) = (2ab,a2-b2,a2+b2) |
|
となります。なぜなら、a は偶数、b は奇数ならば、y2 ≡ 1 (mod 4)(奇数の平方数は4で割ると1余る)を考えると、
a2-b2 ≡ (偶数の平方) - (奇数の平方)(mod 4)
≡ 3(mod 4)
より矛盾するからです。
(a,b)=1 より、
(a,b,y)=1
です。ここで、
|
a2 = b2 + y2 b,y の偶奇は異なる。(a,b,y)=1 |
これは、(*2)の形であらわすことができましたね。そこで、
|
とおきます。ここで、
x2 = 2ab = 4cd(c2+d2)
この、右辺のc,d,(c2+d2)はどの2つも互いに素なので、c,d,(c2+d2)はすべて平方数となります。
(c,d,c2+d2) = (f2,g2,h2)
とおけば、
f4 + g4 = c2+d2 = h2
z2 = x4 + y4 > x4 > x2 = 4cd(c2+d2) > c2+d2 = h2
ここまでくると証明できたも同然ですね。
x4 + y4 = z2
が、いくらでも小さな値を自然数解として持つことになります。無限降下法により、x4 + y4 = z2が、整数解を持たないことが示されたと同時に、n = 4 のときも整数解を持たないことが示されたわけです。
まだまだ続く
